Appendix: Modified Wavenumber

Appendix: Modified Wavenumber#

강좌: 기초 전산유체역학

Modified wavenumber#

  • 정확도를 평가하는 또 다른 방법

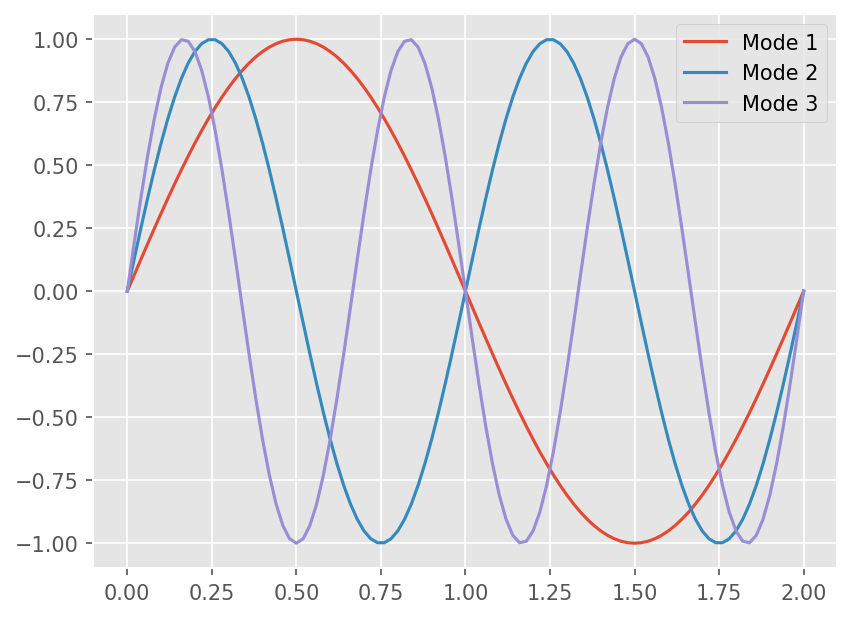
  • 임의의 함수는 Fourier expansion을 이용하면 Sinusoidal 함수로 표현 가능

\[ f(x) = \sum_{n=0}^{\infty} a_n \cos(nx) + b_n \sin(nx) \]

  • \(n\) 이 커질수록 주기가 짧아짐 : High frequency

  • High frequency 항을 모사하기 위해서는 \(\Delta x\) 를 줄이거나 정확도가 높아야 함

  • Finite difference 의 정확도에 따라 Low frequeny 항은 잘 모사할 수 있으나 High frequency 항은 왜곡될 수 있음

%matplotlib inline
from matplotlib import pyplot as plt

import numpy as np

plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150

x = np.linspace(0, 2, 101)

legends = []
for i in range(1, 4):
    plt.plot(x, np.sin(np.pi*i*x))
    legends.append("Mode {}".format(i))
    
plt.legend(legends)

<matplotlib.legend.Legend at 0xff05a98b9390>
../_images/468de4f49cd6d63785f76cfa11192f7f7e6c7eb98ea9d24b49a1d79905fff76c.png

  • Modified wavenumber

    • 간단한 Harmonic 함수에 대해 분석

    \[ f(x) = e^{ikx}, \]

    • \([0, L]\) 영역을 N개의 격자로 나누었다고 생각하자. 이때 waveumber \(k\)를 다음과 같이 고려하자

    \[ k = \frac{2\pi}{L} n, ~~~n=0, 1, 2, ... \frac{N}{2} \]

    • 이론적인 미분은

    \[ f' = ikf \]

    • Finite difference

      • 격자점은

        \[ x_j = \frac{L}{N} j ~~~j=0,1,2,...,N. \]

      • Central differnce에 대해 Harmonic 함수 적용

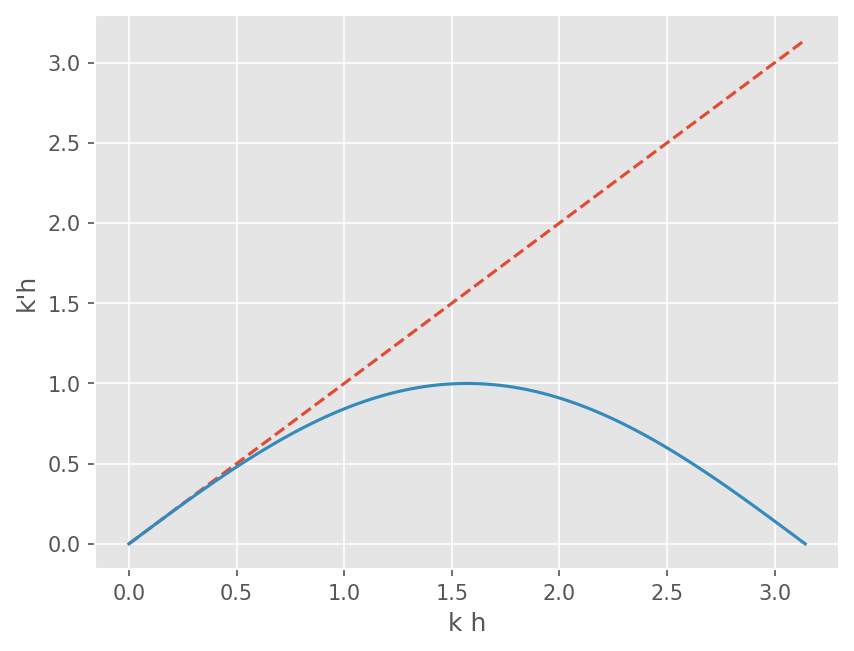
        \[ f'_j = f'(x_j) = \frac{f(x_{j+1}) - f(x_{j-1})}{2\Delta x} = \frac{e^{i 2\pi n (j+1)/N} - e^{i 2\pi n (j-1)/N}}{2\Delta x} = \frac{e^{i 2\pi n /N} - e^{-i 2\pi n /N}}{2\Delta x} f_j \]
        \[ f'_j = i \frac{\sin(2\pi n/N)}{\Delta x} f_j = ik'f_j \]

        즉

        \[ k' \Delta x = \sin(2\pi n/N) = \sin (k \Delta x) \]
kh = np.linspace(0, np.pi, 101)
mkh = np.sin(kh)

plt.plot(kh, kh, linestyle='--')
plt.plot(kh, mkh)
plt.xlabel('k h')
plt.ylabel("k'h")

Text(0, 0.5, "k'h")
../_images/f4c6b709111a1bc24b064417a2a4efacd28ba6c575a1effbb380b3571d3e731e.png 
def forward_diff(f, x, dx):
    # Forward difference
    return (f(x+dx) - f(x)) / dx

def backward_diff(f, x, dx):
    # Backward difference
    return (f(x) - f(x-dx)) / dx

def central_diff(f, x, dx):
    # Central difference
    return (f(x+dx) - f(x-dx)) / (2*dx)

def compute(dx):
    x = np.linspace(0, 2*np.pi, 101)
    f = np.sin

    # Compute first derivatives
    exact = np.cos(x)
    fd = np.array([forward_diff(f, xi, dx) for xi in x])
    bd = np.array([backward_diff(f, xi, dx) for xi in x])
    cd = np.array([central_diff(f, xi, dx) for xi in x])
    
    return x, exact, fd, bd, cd

def plot(dx):
    x, exact, fd, bd, cd = compute(dx)

    # Plot
    plt.plot(x , exact)
    plt.plot(x, fd)
    plt.plot(x, bd)
    plt.plot(x, cd)

    plt.legend(['Exact', 'Forward Difference', 'Backward Difference', 'Central Difference'])
    plt.xlabel(r'x')
    plt.ylabel(r"$f'(x)$")
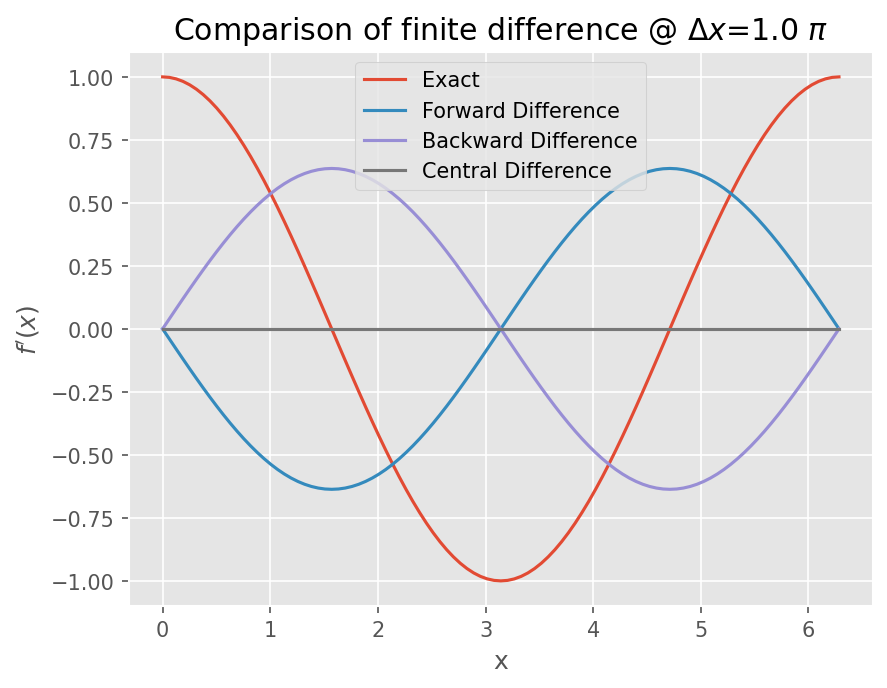
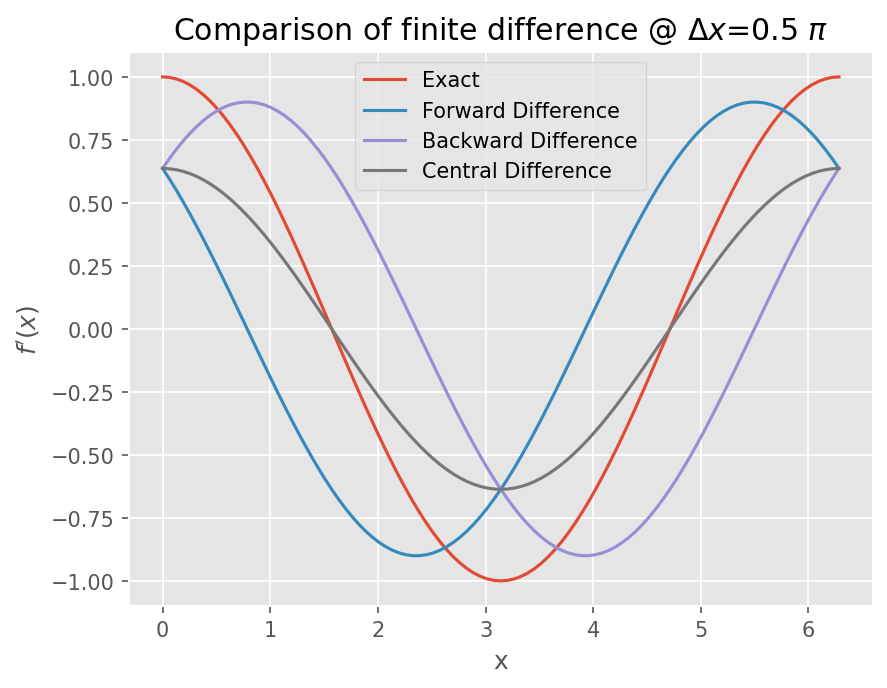
    plt.title("Comparison of finite difference @ $\Delta x$={} $\pi$".format(dx/np.pi))

plot(0.5*np.pi)
../_images/98070a34a780c80f7a6650bd85e47ca9c4eaf53b99468426984be5adfced5ae4.png 
plot(np.pi)
../_images/a8a4534a40de33099f545a2b663cc79912597976970abfb7fe41a02a637af4fb.png
Contents